목차
문제
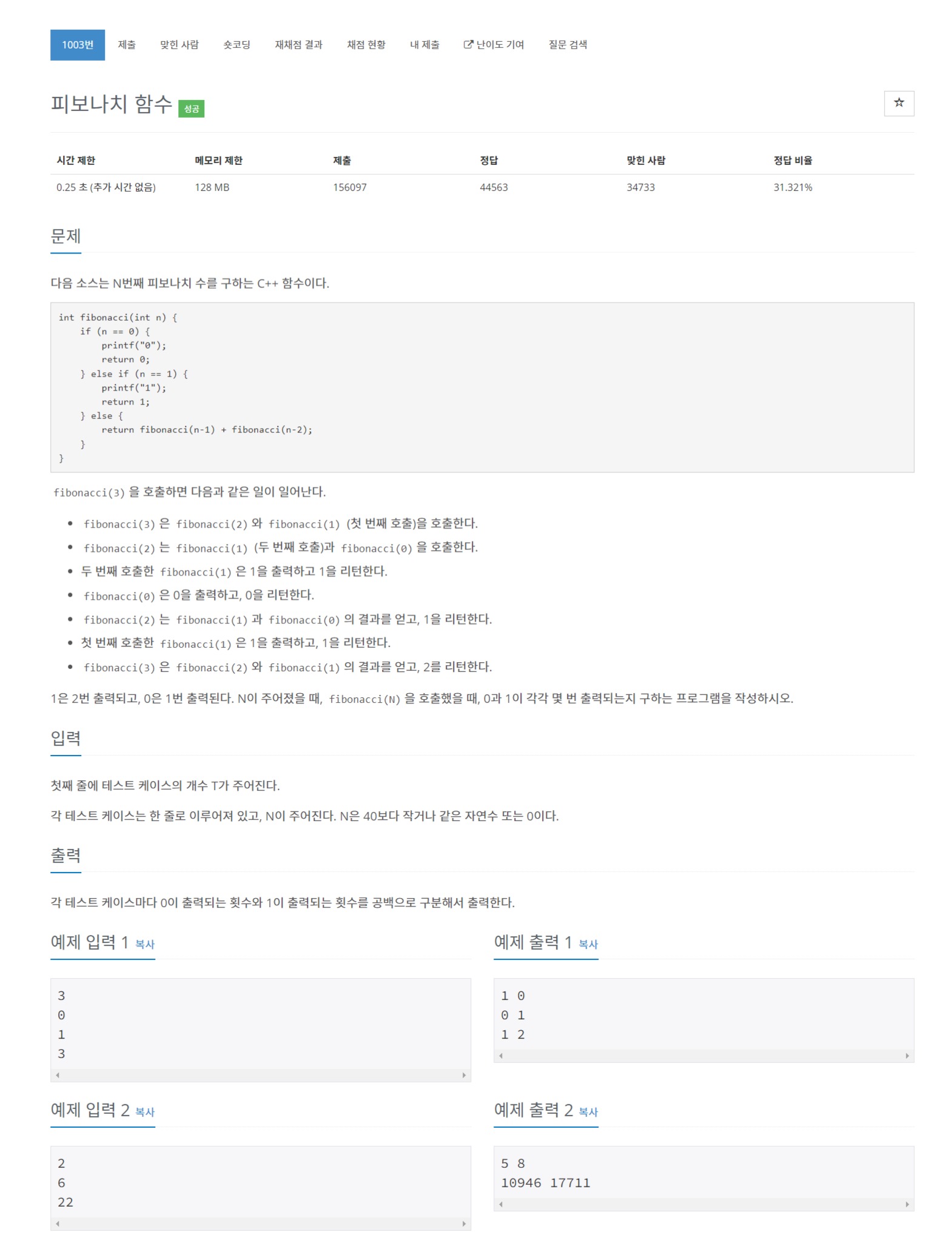
https://www.acmicpc.net/problem/1003
1003번: 피보나치 함수
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
www.acmicpc.net
설계 및 풀이
DP 문제이다.
사실 문제 유형을 어떻게 알아내는지는 좀 더 문제를 풀어봐야 알 것 같다.
처음엔 재귀로 풀었는데, 재귀로 풀다보니 시간 초과가 되어서 뭘까 고민하다가 결국 답지를 봤는데.. DP더라...
먼저, 재귀로 푼 코드다.
cntZero = 0
cntOne = 0
def fibonacci(n):
global cntZero
global cntOne
if n == 0:
cntZero += 1
return 0
elif n == 1:
cntOne += 1
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
T = int(input())
for i in range(T):
n = int(input())
fibonacci(n)
print(cntZero, cntOne)
cntZero = 0
cntOne = 0재귀로 풀면 풀이는 가능한데, 시간 초과가 된다.
이 문제는 단순히 피보나치를 구현하는게 아닌 0과 1이 호출되는 횟수를 구하는 문제이므로, 조금 다르게 접근해보자.
먼저, 문제에서 나온대로 3회를 호출한다고 가정하고, fibonacchi(0) 과 fibonacchi(1) (이하 f(n)으로 표현하겠다) 이 호출되는 횟수를 표로 정리해보면 다음과 같다.
| n의 값 | 0 | 1 | 2 |
| 0이 호출되는 횟수 | 1 | 0 | 1 |
| 1이 호출되는 횟수 | 0 | 1 | 1 |
여기까지는 문제에서 주어지는 예시로 유추할 수 있다. 2번만 더해서 5까지만 해보자.
| n의 값 | 0 | 1 | 2 | 3 | 4 |
| 0이 호출되는 횟수 | 1 | 0 | 1 | 1 | 2 |
| 1이 호출되는 횟수 | 0 | 1 | 1 | 2 | 3 |
어느정도 규칙이 보인다.
0과 1의 호출 횟수 값은 f(n-2) + f(n-1) 이라는 것을 찾을 수 있다.
따라서, 이 식을 그대로 배열의 인덱스에 적용을 해서 답을 풀어봤는데, 다음과 같이 나온다.
# 3까지는 문제를 통해서 유추 가능하므로 3까지 하드코딩
cntZero = [1, 0, 1]
cntOne = [0, 1, 1]
def fibonacci(n):
#2번 index까지는 그냥 노출
if n < 3:
print(cntZero[n], cntOne[n])
else:
#3번째 이상은 배열에 없으니 추가해주기
for i in range(3, n + 1):
cntZero.append(cntZero[i-2] + cntZero[i-1])
cntOne.append(cntOne[i-2] + cntOne[i-1])
print(cntZero[n], cntOne[n])
T = int(input())
for i in range(T):
n = int(input())
fibonacci(n)그런데 정답이 아니었다. 왜인지 알아보니까, 여러번 답을 입력하면, 이전에 입력했던 값이 남아있어서 라고 한다.
for문에 있는 하드코딩을 바꾸고, 길이에 따라가도록 length로 조건을 걸어주니 정답처리가 됐다..
근데 사실 말만 다르지 같은 로직이지않나..? 왜 틀렸는지는 좀 더 고민을 해봐야 알 것 같다.
내가 올린 질문을 링크한다. 참고!
https://www.acmicpc.net/board/view/88522
글 읽기 - 어디가..틀린걸까요 ㅠㅠ
댓글을 작성하려면 로그인해야 합니다.
www.acmicpc.net
코드 GIT 주소
Algorithm_study/220415_1003.py at main · kkkapuq/Algorithm_study (github.com)
GitHub - kkkapuq/Algorithm_study: 알고리즘 문제풀이
알고리즘 문제풀이. Contribute to kkkapuq/Algorithm_study development by creating an account on GitHub.
github.com
코드
# 3까지는 문제를 통해서 유추 가능하므로 3까지 하드코딩
cntZero = [1, 0, 1]
cntOne = [0, 1, 1]
def fibonacci(n):
#2번 index까지는 그냥 노출
length = len(cntZero)
if n >= length:
for i in range(length, n + 1):
cntZero.append(cntZero[i-2] + cntZero[i-1])
cntOne.append(cntOne[i-2] + cntOne[i-1])
print(cntZero[n], cntOne[n])
T = int(input())
for i in range(T):
n = int(input())
fibonacci(n)
결과
구독 및 하트는 정보 포스팅 제작에 큰 힘이됩니다♡
'PS, 언어 공부 > 알고리즘 문제풀이' 카테고리의 다른 글
| [Python] 백준 온라인 저지 1764 (0) | 2022.05.06 |
|---|---|
| [알고리즘 이론] 다익스트라(Dijkstra), 최단 경로 알고리즘 (0) | 2022.04.24 |
| [C++] 백준 온라인 저지 2869 (0) | 2020.09.16 |
| [C++] 백준 온라인 저지 2292 (0) | 2020.09.09 |
| [C++] 백준 온라인 저지 1712 (0) | 2020.09.08 |